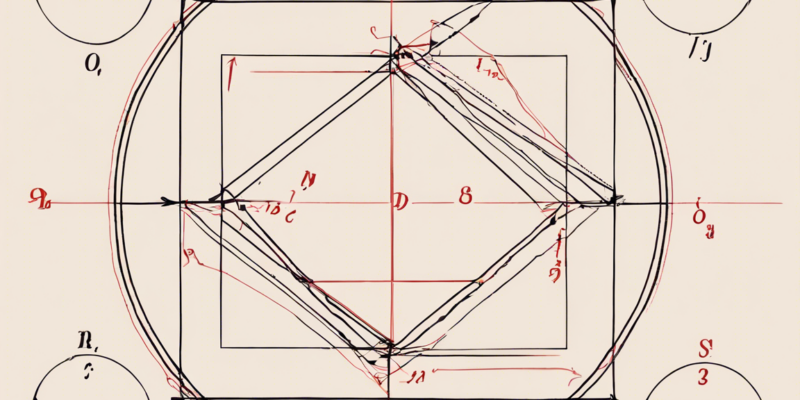
Parallelogram Circumscribing a Circle is Rhombus!
In the realm of geometry, there are numerous fascinating relationships and properties among shapes and figures. One such intriguing connection involves a parallelogram that circumscribes a circle, ultimately resulting in the creation of a rhombus. This phenomenon showcases the interplay between different geometric shapes and provides valuable insights into their inherent properties and characteristics. In this comprehensive article, we will delve into the intricacies of this relationship, exploring the key concepts, definitions, and proofs that underpin this geometric phenomenon.
Understanding the Parallelogram Circumscribing a Circle
To begin our exploration, let us first establish a clear understanding of the parallelogram and the concept of circumscribing a circle. A parallelogram is a quadrilateral with opposite sides that are parallel and equal in length. This fundamental geometric shape possesses several unique properties, including symmetry, equal opposite angles, and diagonal bisecting each other.
On the other hand, when we refer to a circle being circumscribed by a parallelogram, we are essentially describing a situation where the circle is enclosed within the boundaries of the parallelogram in such a way that the circle touches each side of the parallelogram at exactly one point. This configuration forms the basis of the relationship we are about to explore.
The Emergence of a Rhombus
As the circle is circumscribed by the parallelogram, a series of compelling geometric transformations unfold, ultimately leading to the formation of a rhombus. A rhombus is a special type of quadrilateral characterized by four sides of equal length and opposite angles that are equal. This elegant shape embodies symmetry and balance, making it a captivating subject of geometric study.
The key to understanding why a rhombus emerges when a circle is circumscribed by a parallelogram lies in the properties of both shapes and their intricate interplay. Through a series of geometric constructions and logical deductions, it can be proven that the resulting quadrilateral formed by the points of tangency between the circle and the sides of the parallelogram is indeed a rhombus.
Proving the Relationship
To substantiate the claim that a parallelogram circumscribing a circle is indeed a rhombus, we can engage in a deductive proof that leverages the properties of circles, parallelograms, and rhombuses. By carefully examining the symmetries, angles, and side lengths inherent in both the circle and the parallelogram, we can establish a rigorous argument that demonstrates the validity of this geometric relationship.
One approach to proving this relationship involves constructing perpendicular bisectors from the points of tangency on the sides of the parallelogram to the center of the circumscribed circle. By leveraging the properties of circles and perpendicular bisectors, we can establish that the resulting quadrilateral formed by these bisectors is a rhombus. This approach highlights the elegance and precision of geometric proofs and underscores the interconnectedness of different geometric shapes.
Exploring Further Implications and Applications
Beyond the specific geometric relationship between a parallelogram circumscribing a circle and the emergence of a rhombus, this phenomenon has broader implications and applications in various branches of mathematics and science. The insights gained from studying these relationships can be applied to fields such as architecture, engineering, computer graphics, and physics, where geometric principles play a fundamental role.
For example, the concept of circumscribing shapes within other shapes is often utilized in industrial design and architectural planning to optimize space utilization and structural integrity. By understanding the properties of circumscribed shapes such as the rhombus within parallelograms, designers and engineers can make informed decisions that enhance the efficiency and robustness of their designs.
FAQs
- What is a parallelogram?
-
A parallelogram is a quadrilateral with opposite sides that are parallel and equal in length.
-
What does it mean for a circle to be circumscribed by a parallelogram?
-
Circumscribing a circle by a parallelogram entails enclosing the circle within the boundaries of the parallelogram in such a way that the circle touches each side of the parallelogram at exactly one point.
-
What is a rhombus?
-
A rhombus is a quadrilateral with four sides of equal length and opposite angles that are equal.
-
How can we prove that a circle circumscribed by a parallelogram forms a rhombus?
-
By constructing perpendicular bisectors from the points of tangency on the sides of the parallelogram to the center of the circle, we can establish that the resulting quadrilateral is a rhombus.
-
What are the applications of understanding the relationship between parallelograms, circles, and rhombuses?
- The insights gained can be applied in various fields such as architecture, engineering, computer graphics, and physics to enhance design efficiency and structural integrity.
In conclusion, the intricate relationship between a parallelogram circumscribing a circle and the emergence of a rhombus exemplifies the elegance and complexity of geometric phenomena. By exploring the properties, constructions, and proofs associated with this relationship, we gain valuable insights into the interconnected nature of geometric shapes and their applications in diverse fields. This captivating geometric relationship serves as a testament to the beauty and versatility of mathematical principles in unraveling the mysteries of the physical world.